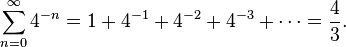ARQUÍMIDES

Arquímedes de Siracusa fue un matemático griego, físico, ingeniero, inventor y astrónomo. Aunque se conocen pocos detalles de su vida, es considerado uno de los científicos más importantes de la antigüedad clásica.

-Arquímedes fue capaz de utilizar los infinitesimales de forma similar al moderno cálculo integral. A través de la reducción al absurdo, era capaz de contestar problemas mediante aproximaciones con determinado grado de precisión, especificando los límites entre los cuales se encontraba la respuesta correcta. Para ello, dibujó un polígono regular inscrito y otro circunscrito a una misma circunferencia, de manera que la longitud de la circunferencia y el área del círculo quedan acotadas por esos mismos valores de las longitudes y las áreas de los dos polígonos.

-En su obra sobre la Medición del Círculo, Arquímedes ofrece un intervalo para el valor de la raíz cuadrada de 3 de entre ²⁶⁵/₁₅₃ (aproximadamente 1,7320261) y ¹³⁵¹/₇₈₀ (aproximadamente 1,7320512). El valor real se ubica aproximadamente en 1,7320508, por lo que la estimación de Arquímedes resultó ser muy exacta. Sin embargo, introdujo este resultado en su obra sin explicación de qué método había utilizado para obtenerlo.

-En su obra sobre La cuadratura de la Parábola, Arquímedes probó que el área definida por una parábola y una línea recta equivalía exactamente a ⁴/₃ el área del correspondiente triángulo inscrito, tal y como se puede observar en la figura de la derecha. Para obtener ese resultado, desarrolló una serie geométrica infinita con una razón común de ¹/₄:

Euclides De Alejandría

Euclides fue un matemático y geometra griego. Se le conoce como "El Padre de la Geometría". Su obra los elementos, es una de las obras científicas más conocidas del mundo y era una recopilación del conocimiento impartido en el centro académico. En ella se presenta de manera formal, partiendo únicamente de cinco postulados, el estudio de las propiedades de líneas y planos, círculos y esferas, triángulos y conos, etc.; es decir, de las formas regulares. Los teoremas de Euclides son los que generalmente se aprenden en la escuela moderna. Por citar algunos de los más conocidos:

• La suma de los ángulos interiores de cualquier triángulo es 180°.
• En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, que es el famoso teorema de Pitagoras
  

TALES DE MILETO

Tales de Mileto es considerado por la tradición historiográfica occidental como el iniciador de la indagación filosófico-científica acerca del cosmos, distinguiéndose por ofrecer las primeras explicaciones registradas respecto de eventos naturales que no apelan a entidades divinas sino que se sustentan en observaciones e inferencias pasibles de ser constatadas y discutidas. Es señalado, entonces, como el primer gran impulsor en Grecia de la investigación cienctífica y como el primer filósofo de la historia de la filosofía occidental, estando a él relacionados Anaximandro -quien habría sido su discípulo- y Anaxímenes -quien habría sido discípulo de este último-, denominándose tradicionalmente al conjunto de los tres como la "escuela jonica" o "de Mileto".

Se atribuyen a Tales varios descubrimientos matemáticos registrados en los Elementos de Euclides:

El primero de ellos explica esencialmente una forma de construir un triángulo semejante a uno previamente existente (los triángulos semejantes son los que tienen iguales ángulos).


 Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos (encontrándose éstos en el punto medio de su hipotenusa), que a su vez en la construcción geométrica es ampliamente utilizado para imponer condiciones de construcción de ángulos rectos. Si tres o más rectas paralelas son intersecadas cada una por dos transversales, los segmentos de las transversales determinados por las paralelas, son proporcionales.

PITÁGORAS

Pitágoras fue un filosofo y matemático griego considerado el primer matemático puro. Contribuyó de manera significativa en el avance de la matemática helénica, la geometría y la aritmética, derivadas particularmente de las relaciones numéricas, y aplicadas por ejemplo a la teoría de pesos y medidas.
La practicada por Pitágoras y los matemáticos difiere del tratamiento de esta ciencia que se lleva a cabo en universidades o instituciones modernas.

 Pitágoras reconocía en los números propiedades tales como «personalidad», «masculinos y femeninos», «perfectos o imperfectos», «bellos y feos». El número diez era especialmente valorado, por ser la suma de los primeros cuatro enteros [1 + 2 + 3 + 4 = 10], los cuales se pueden disponer en forma de triángulo perfecto.

Entre los descubrimientos matemáticos que se atribuyen a la escuela de Pitágoras se encuentran el teorema de pitágoras entre los mas destacados
 * Teorema de pitágoras: 

En un triángulo rectángulo: «la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa». Si bien este resultado y las ternas pitágoricas eran conceptos ya conocidos y utilizados por los matemáticos babilonios y de la India desde mucho tiempo