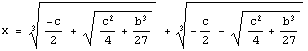Scipione del Ferro

Scipione del Ferro ha sido un matemático italiano, a la que se debe el primer método determinante para las ecuaciones de tercer grado.Scipione del Ferro se educó en la Universidad de Bolonia que fue fundada en el siglo XI.No han sobrevivido escritos de del Ferro, ello se debe a la resistencia que tenía a divulgar sus trabajos, prefería comunicarlos a un reducido grupo de alumnos y amigos. Se cree que tenía algún manuscrito donde guardaba sus importantes descubrimientos. Este manuscrito pasó al yerno, Annibale Nave, cuando del Ferro murió en 1526. Que también se dedicó a la Matemática y lo reemplazó como catedrático, cuando falleció, en la Universidad de Bolonia.
Hoy se cree que del Ferro sólo podía resolver cúbicas de esa forma x^3 + mx = n, con m y n positivos. Hoy día también se sabe, que el caso general, y^3 - by2 + cy - d = 0, se reduce a este por medio del cambio lineal y = x + b/3. Obteniéndose la cúbica reducida anterior con los valores m = c - b/3, n = d - bc/3 + 2b/27.
En notación moderna la solución de la cúbica reducida x^3 + bx = c se obtiene de la siguiente forma: sea x=y-z, entonces (y-z)^3=y^3-z^3-3y^2z+3yz^2. Sacando factor común a 3yz, y pasando al primer miembro, se obtiene (y-z)^3+3yz(y-z)=y^3-z^3. Donde se puede identificar los coeficientes b=3yz, c=y^3-z^3.
De donde, z = b/3y, lo podemos sustituir en la otra igualdad, obteniendo y^3- b^3/27y^3 = c. O sea, y^6 -cy^3 - b^3/27 =0. De donde podemos obtener el valor de y^3, resolviendo la ecuación cuadrática t^2-ct - b^3/27 =0 y sustituyendo ese valor en z = b/3y. Restando finalmente ambos valores obtenemos una solución de la cúbica reducida. Fórmula hoy día conocida como del Ferro-Tartaglia:

LUCA PACIOLI

Luca Pacioli fue un fraile franciscano y matemático italiano, precursor del cálculo de probabilidades. Analizó sistemáticamente el método contable de la partida doble usado por los comerciantes venecianos en su obra Summa de arithmetica, geometria, proportioni et proportionalita (Venecia, 1494), que a pesar de su título latino, incluye la primera obra matemática impresa en lengua romance.
Su obra más divulgada e influyente es De Divina Proportione (De la Divina Proporción) término relativo a la razón o proporción ligada al denominado número áureo, escrita en Milán entre 1496 y 1498, y que trata también, en su primera parte, de los polígonos y la perspectiva usada por los pintores del Quattrocento (Compendio Divina Proportione); en su segunda, de las ideas arquitectónicas de Vitruvio (Summa de arithmetica, geometria, proportioni et proportionalita); y en su tercera, de los sólidos platónicos o regulares (De quinque corporibus regularibus).

Fibonacci, Leonardo De Pisa

Fibonacci, Leonardo De Pisa fue un matemático italiano, famoso por haber difundido en Europa el sistema de numeración indo-arábigo actualmente utilizado. Fibonacci viajó a través de los países del Mediterráneo para estudiar con los matemáticos árabes más destacados de esos tiempos. en 1202 publicó lo que había aprendido em el Liber Abaci.

DIOFANTO DE ALEJANDRÍA

Diofanto de Alejandría fue un antiguo matemático griego. Es considerado "el padre del álgebra". El matemático alejandrino debe su renombre a su obra Arithmetica. Este libro, que constaba de trece libros de los que sólo se han hallado seis. En esta obra realiza sus estudios de ecuaciones con variables que tienen un valor racional (ecuaciones diofánticas), aunque no es una obra de carácter teórico sino una colección de problemas.