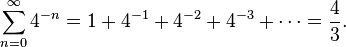Nicolás Copérnico fue un astrónomo polaco del Renacimiento que formuló la teoría heliocéntrica del Sistema Solar, concebida en primera instancia por Aristarco de Samos. Su libro, De revolutionibus orbium coelestium (Sobre las revoluciones de las esferas celestes),
suele estar considerado como el punto inicial o fundador de la
astronomía moderna, además de ser una pieza clave en lo que se llamó la Revolución Científica en la época del Renacimiento.
Copérnico pasó cerca de veinticinco años trabajando en el desarrollo de
su modelo heliocéntrico del universo. En aquella época resultó difícil
que los científicos lo aceptaran, ya que suponía una auténtica
revolución.
Copérnico era un polímata: matemático, astrónomo, jurista, físico, clérigo católico, gobernador, administrador, líder militar, diplomático y economista.
Junto con sus extensas responsabilidades, la astronomía figuraba como
poco más que una distracción. Por su enorme contribución a la
astronomía, en 1935 se dio el nombre «Copernicus» a uno de los mayores cráteres lunares, ubicado en el Mare Insularum.En 1492, cuando Colón descubría América y abría un nuevo mundo geográfico, Copérnico se matriculó en la Universidad de
Cracovia, en Polonia, uno de los centros más distinguidos de cultura de esa época. Quedó bajo la tutela de Alberto
Brudzewski, notable matemático y astrónomo, que cultivó el profundo interés de Nicolás por esas materias. Sin embargo, por
consejo de su tío, el obispo, Nicolás se licenció en medicina, a fin de prestar una ayuda más directa a sus compatriotas.
La obra de Nicolás en Cracovia le abrió las puertas de la cultura. Le preguntó a su tío si podía continuar sus estudios en
Italia, centro de aprendizaje y cuna del Renacimiento. Prudentemente su tío consistió e hizo los arreglos necesarios para que
asistiera a la famosa Universidad de Bolonia, donde estudió derecho y amplió sus conocimientos de matemáticas y
astronomía. También aprendió griego a fin de leer los textos originales de los astrónomos griegos, así como sus traducciones
de los antiguos matemáticos árabes Copérnico también desarrolló sus aptitudes como pintor y poeta.
matematicos famosos
jueves, 7 de marzo de 2013
jueves, 28 de febrero de 2013
Scipione del Ferro
Scipione del Ferro ha sido un matemático italiano, a la que se debe el primer método
determinante para las ecuaciones de tercer grado.Scipione del Ferro se educó en la Universidad de Bolonia que fue fundada en el siglo XI.No han sobrevivido escritos de del Ferro, ello se debe a la resistencia
que tenía a divulgar sus trabajos, prefería comunicarlos a un reducido
grupo de alumnos y amigos. Se cree que tenía algún manuscrito donde
guardaba sus importantes descubrimientos. Este manuscrito pasó al yerno,
Annibale Nave, cuando del Ferro murió en 1526. Que también se dedicó a
la Matemática y lo reemplazó como catedrático, cuando falleció, en la
Universidad de Bolonia.
Hoy se cree que del Ferro sólo podía resolver cúbicas de esa forma x^3 + mx = n, con m y n positivos. Hoy día también se sabe, que el caso general, y^3 - by2 + cy - d = 0, se reduce a este por medio del cambio lineal y = x + b/3. Obteniéndose la cúbica reducida anterior con los valores m = c - b/3, n = d - bc/3 + 2b/27.
En notación moderna la solución de la cúbica reducida x^3 + bx = c se obtiene de la siguiente forma: sea x=y-z, entonces (y-z)^3=y^3-z^3-3y^2z+3yz^2. Sacando factor común a 3yz, y pasando al primer miembro, se obtiene (y-z)^3+3yz(y-z)=y^3-z^3. Donde se puede identificar los coeficientes b=3yz, c=y^3-z^3.
De donde, z = b/3y, lo podemos sustituir en la otra igualdad, obteniendo y^3- b^3/27y^3 = c. O sea, y^6 -cy^3 - b^3/27 =0. De donde podemos obtener el valor de y^3, resolviendo la ecuación cuadrática t^2-ct - b^3/27 =0 y sustituyendo ese valor en z = b/3y. Restando finalmente ambos valores obtenemos una solución de la cúbica reducida. Fórmula hoy día conocida como del Ferro-Tartaglia:
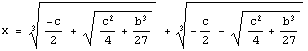
Hoy se cree que del Ferro sólo podía resolver cúbicas de esa forma x^3 + mx = n, con m y n positivos. Hoy día también se sabe, que el caso general, y^3 - by2 + cy - d = 0, se reduce a este por medio del cambio lineal y = x + b/3. Obteniéndose la cúbica reducida anterior con los valores m = c - b/3, n = d - bc/3 + 2b/27.
En notación moderna la solución de la cúbica reducida x^3 + bx = c se obtiene de la siguiente forma: sea x=y-z, entonces (y-z)^3=y^3-z^3-3y^2z+3yz^2. Sacando factor común a 3yz, y pasando al primer miembro, se obtiene (y-z)^3+3yz(y-z)=y^3-z^3. Donde se puede identificar los coeficientes b=3yz, c=y^3-z^3.
De donde, z = b/3y, lo podemos sustituir en la otra igualdad, obteniendo y^3- b^3/27y^3 = c. O sea, y^6 -cy^3 - b^3/27 =0. De donde podemos obtener el valor de y^3, resolviendo la ecuación cuadrática t^2-ct - b^3/27 =0 y sustituyendo ese valor en z = b/3y. Restando finalmente ambos valores obtenemos una solución de la cúbica reducida. Fórmula hoy día conocida como del Ferro-Tartaglia:
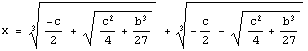
jueves, 21 de febrero de 2013
LUCA PACIOLI
Luca Pacioli fue un fraile franciscano y matemático italiano, precursor del cálculo de probabilidades. Analizó sistemáticamente el método contable de la partida doble usado por los comerciantes venecianos en su obra Summa de arithmetica, geometria, proportioni et proportionalita (Venecia, 1494), que a pesar de su título latino, incluye la primera obra matemática impresa en lengua romance.
Su obra más divulgada e influyente es De Divina Proportione (De la Divina Proporción) término relativo a la razón o proporción ligada al denominado número áureo, escrita en Milán entre 1496 y 1498, y que trata también, en su primera parte, de los polígonos y la perspectiva usada por los pintores del Quattrocento (Compendio Divina Proportione); en su segunda, de las ideas arquitectónicas de Vitruvio (Summa de arithmetica, geometria, proportioni et proportionalita); y en su tercera, de los sólidos platónicos o regulares (De quinque corporibus regularibus).
Su obra más divulgada e influyente es De Divina Proportione (De la Divina Proporción) término relativo a la razón o proporción ligada al denominado número áureo, escrita en Milán entre 1496 y 1498, y que trata también, en su primera parte, de los polígonos y la perspectiva usada por los pintores del Quattrocento (Compendio Divina Proportione); en su segunda, de las ideas arquitectónicas de Vitruvio (Summa de arithmetica, geometria, proportioni et proportionalita); y en su tercera, de los sólidos platónicos o regulares (De quinque corporibus regularibus).
viernes, 15 de febrero de 2013
Fibonacci, Leonardo De Pisa
Fibonacci, Leonardo De Pisa fue un matemático italiano, famoso por haber difundido en Europa el sistema de numeración indo-arábigo actualmente utilizado. Fibonacci viajó a través de los países del Mediterráneo para estudiar con los matemáticos árabes más destacados de esos tiempos. en 1202 publicó lo que había aprendido em el Liber Abaci.
jueves, 14 de febrero de 2013
DIOFANTO DE ALEJANDRÍA
 Diofanto de Alejandría fue un antiguo matemático griego. Es considerado "el padre del álgebra". El matemático alejandrino debe su renombre a su obra Arithmetica. Este libro, que constaba de trece libros de los que sólo se han hallado seis. En esta obra realiza sus estudios de ecuaciones con variables que tienen un valor racional (ecuaciones diofánticas), aunque no es una obra de carácter teórico sino una colección de problemas.
Diofanto de Alejandría fue un antiguo matemático griego. Es considerado "el padre del álgebra". El matemático alejandrino debe su renombre a su obra Arithmetica. Este libro, que constaba de trece libros de los que sólo se han hallado seis. En esta obra realiza sus estudios de ecuaciones con variables que tienen un valor racional (ecuaciones diofánticas), aunque no es una obra de carácter teórico sino una colección de problemas.
jueves, 31 de enero de 2013
ARQUÍMIDES
Arquímedes de Siracusa fue un matemático griego, físico, ingeniero, inventor y astrónomo. Aunque se conocen pocos detalles de su vida, es considerado uno de los científicos más importantes de la antigüedad clásica.
-Arquímedes fue capaz de utilizar los infinitesimales de forma similar al moderno cálculo integral. A través de la reducción al absurdo, era capaz de contestar problemas mediante aproximaciones con determinado grado de precisión, especificando los límites entre los cuales se encontraba la respuesta correcta. Para ello, dibujó un polígono regular inscrito y otro circunscrito a una misma circunferencia, de manera que la longitud de la circunferencia y el área del círculo quedan acotadas por esos mismos valores de las longitudes y las áreas de los dos polígonos.
-En su obra sobre la Medición del Círculo, Arquímedes ofrece un intervalo para el valor de la raíz cuadrada de 3 de entre 265/153 (aproximadamente 1,7320261) y 1351/780 (aproximadamente 1,7320512). El valor real se ubica aproximadamente en 1,7320508, por lo que la estimación de Arquímedes resultó ser muy exacta. Sin embargo, introdujo este resultado en su obra sin explicación de qué método había utilizado para obtenerlo.
-En su obra sobre La cuadratura de la Parábola, Arquímedes probó que el área definida por una parábola y una línea recta equivalía exactamente a 4/3 el área del correspondiente triángulo inscrito, tal y como se puede observar en la figura de la derecha. Para obtener ese resultado, desarrolló una serie geométrica infinita con una razón común de 1/4:
-Arquímedes fue capaz de utilizar los infinitesimales de forma similar al moderno cálculo integral. A través de la reducción al absurdo, era capaz de contestar problemas mediante aproximaciones con determinado grado de precisión, especificando los límites entre los cuales se encontraba la respuesta correcta. Para ello, dibujó un polígono regular inscrito y otro circunscrito a una misma circunferencia, de manera que la longitud de la circunferencia y el área del círculo quedan acotadas por esos mismos valores de las longitudes y las áreas de los dos polígonos.
-En su obra sobre la Medición del Círculo, Arquímedes ofrece un intervalo para el valor de la raíz cuadrada de 3 de entre 265/153 (aproximadamente 1,7320261) y 1351/780 (aproximadamente 1,7320512). El valor real se ubica aproximadamente en 1,7320508, por lo que la estimación de Arquímedes resultó ser muy exacta. Sin embargo, introdujo este resultado en su obra sin explicación de qué método había utilizado para obtenerlo.
-En su obra sobre La cuadratura de la Parábola, Arquímedes probó que el área definida por una parábola y una línea recta equivalía exactamente a 4/3 el área del correspondiente triángulo inscrito, tal y como se puede observar en la figura de la derecha. Para obtener ese resultado, desarrolló una serie geométrica infinita con una razón común de 1/4:
jueves, 24 de enero de 2013
Euclides De Alejandría
Euclides fue un matemático y geometra griego. Se le conoce como "El Padre de la Geometría". Su obra los elementos,
es una de las obras científicas más conocidas del mundo y era una
recopilación del conocimiento impartido en el centro académico. En ella
se presenta de manera formal, partiendo únicamente de cinco postulados,
el estudio de las propiedades de líneas y planos, círculos y esferas,
triángulos y conos, etc.; es decir, de las formas regulares. Los teoremas de Euclides son los que generalmente se aprenden en la escuela moderna. Por citar algunos de los más conocidos:
Suscribirse a:
Entradas (Atom)